20240730 TIL
확률변수
- 어떤 확률 실험이나 상황에서 발생할 수 있는 각각의 결과를 수치적 값으로 표현하는 변수
= 확률변수는 표본 공간에 있는 모든 원소들을 수치적 값(실수)으로 만드는 함수
확률분포
- 확률변수가 특정 값들을 가질 확률을 나타내는 함수(=확률함수)
= 확률이 만들어지는 확률 함수가 그리는 패턴
이산확률분포
-각 분포의 종류와 특징 알기
-값이 하나씩 떨어져 있는 것(확률질량함수)
▶ 베르누이 분포 - 확률 변수가 0 또는 1 두개의 결과만 갖는 분포
▶ 이항분포 - n번의 베르누이 시행(성공 또는 실패)에서 k번 성공할 확률의 분포
▶ 기하분포 - 성공확률이 p인 베르누이 시행에서 첫 번째 성공이 있기까지 k번 실패할 확률(=첫 성공이 일어나기 위해 필요한 시행횟수)
▶ 다항분포 - n번의 시행에서 각 시행이 3개 이상의 결과를 가질 수 있는 확률 분포
▶ 포아송 분포 - 시간과 공간 내에서 발생하는 사건의 발생 횟수에 대한 확률 분포
연속확률분포
-값이 연속적(확률밀도함수)
*이산형 -> 셀 수 있음 : 더하면 된다 -> ∑(시그마)
*연속형 -> 셀 수 없음 : 구간 -> ∫
--> ADsP에서는 기호함수로 구분 가능!
▶ 균일분포 - 모든 확률변수 X가 균일한 확률을 가지는 확률 분포(어떠한 특정 구간이 주어져도 확률이 일정!)

▶ 정규분포 - 표준편차가 클 경우 퍼져보인느 그래프(표준편차에 따라 그래프가 달라짐), 일반적인 데이터 분포 중 가장 일반적인 분포

▶ t-분포 - 통계적으로 표본으로부터 모집단의 평균에 대한 추정을 할 때 사용되는 분포
자유도란? 표본자료들이 모집단에 대한 정보를 주는 독립적인 자료의 개수를 의미
ex) 사탕 4개와 사람 4명이 있을 때 앞의 3명까지는 원하는 사탕 선택 가능 하지만 마지막 사람은 선택권이 없기 때문에 남은 사탕을 가져갈 수 밖에 없다. 따라서 자유도는 4명에서 하나 적은 3이 된다

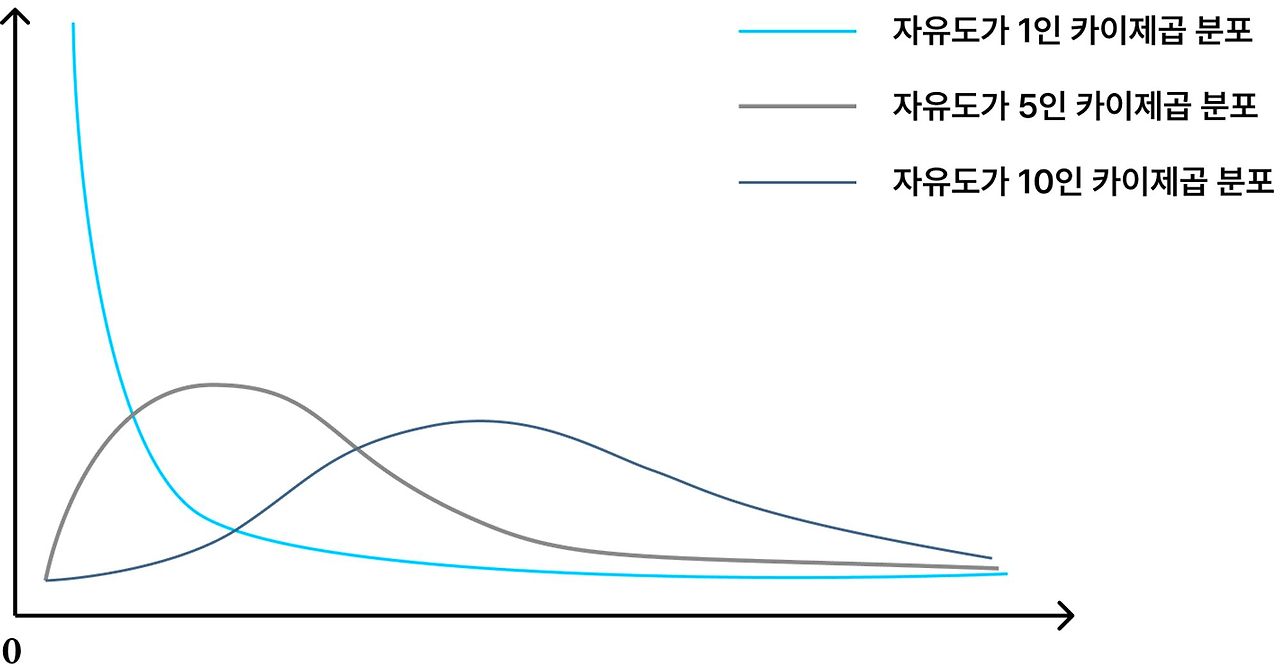
▶ 카이제곱 분포 - 표준정규분포(=의 분산에 대한 분포)를 따르는 확률변수들의 제곱을 합한 분포
* 분산이 1일 때 가장 이상적
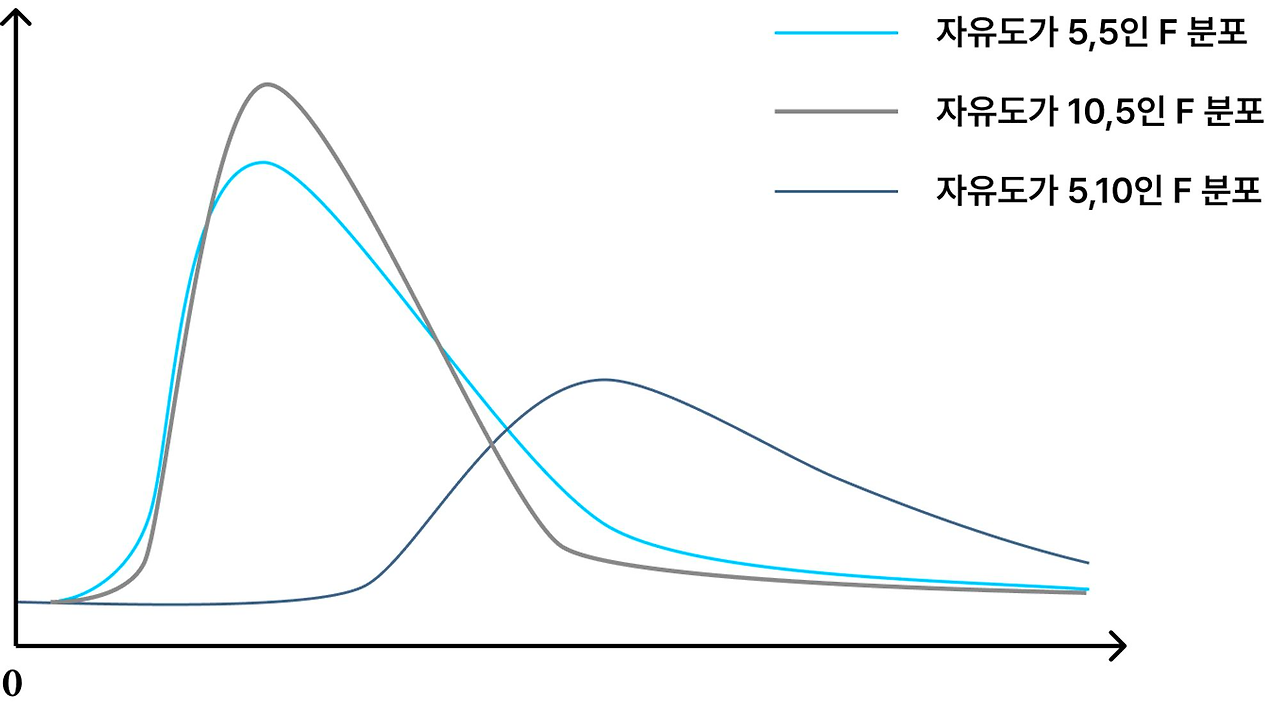
▶ F 분포(=카이스퀘어의 비율을 따르고 있는 것) - 두 집단 간 분산의 동일성 검정에 사용되는 검정 통계량의 분포
항상 양의 값, 카이스퀘어 분포와 달리 자유도를 2개 가지고 있으며 자유도가 커질수록 정규분포에 가까워진다
3과목부터는 굉장히 여러번 본 것 같다. 통계에 대한 내용은 학생때 배웠던 것 같은데 잘 기억이 나질 않는다 ... !
이제 진짜 시험날까지 얼마 남지 않았는데 기초프로젝트도 내일이면 완전히 끝나기 때문에 ADsP에 좀 집중을 해야 할 것 같다
1, 2과목은 반복적으로 개념을 읽어주는게 좋을 것 같고 3과목은 여러 번 반복해서 강의를 들어야 할 것 같다.
그래도 여러 번 들으니 조금씩 이해돼서 나름 뿌듯하다 !! 남은 기간동안에도 화이팅
