20240828 TIL
4. 이상치 제거
▶ IQR 작업 --> 이상치 제거법
- Dept 이상치 제거
# Dept 이상치 제거
pct25 = df['Dept'].quantile(.25)
pct75 = df['Dept'].quantile(.75)
iqr = pct75 - pct25
pct25 - 1.5 * iqr # 하한
pct75 + 1.5 * iqr # 상한
df['Dept'] = np.where((df['Dept']<pct25 - 1.5 * iqr) | (df['Dept']>pct75 + 1.5 * iqr), np.nan, df['Dept'])
df = df.dropna(subset='Dept')
df.head(3)- Size 이상치 제거
# Size 이상치 제거
pct25 = df['Size'].quantile(.25)
pct75 = df['Size'].quantile(.75)
iqr = pct75 - pct25
pct25 - 1.5 * iqr # 하한
pct75 + 1.5 * iqr # 상한
df['Size'] = np.where((df['Size']<pct25 - 1.5 * iqr) | (df['Size']>pct75 + 1.5 * iqr), np.nan, df['Size'])
df = df.dropna(subset='Size')
df.head(3)- Store 이상치 제거
# Store 이상치 제거
pct25 = df['Store'].quantile(.25)
pct75 = df['Store'].quantile(.75)
iqr = pct75 - pct25
pct25 - 1.5 * iqr # 하한
pct75 + 1.5 * iqr # 상한
df['Store'] = np.where((df['Store']<pct25 - 1.5 * iqr) | (df['Store']>pct75 + 1.5 * iqr), np.nan, df['Store'])
df = df.dropna(subset='Store')
df.head(3)- CPI 이상치 제거
# CPI 이상치 제거
pct25 = df['CPI'].quantile(.25)
pct75 = df['CPI'].quantile(.75)
iqr = pct75 - pct25
pct25 - 1.5 * iqr # 하한
pct75 + 1.5 * iqr # 상한
df['CPI'] = np.where((df['CPI']<pct25 - 1.5 * iqr) | (df['CPI']>pct75 + 1.5 * iqr), np.nan, df['CPI'])
df = df.dropna(subset='CPI')
df.head(3)-Fuel_Price 이상치 제거
# Fuel_Price 이상치 제거하기
pct25 = df['Fuel_Price'].quantile(.25)
pct75 = df['Fuel_Price'].quantile(.75)
iqr = pct75 - pct25
pct25 - 1.5 * iqr # 하한
pct75 + 1.5 * iqr # 상한
df['Fuel_Price'] = np.where((df['Fuel_Price']<pct25 - 1.5 * iqr) | (df['Fuel_Price']>pct75 + 1.5 * iqr), np.nan, df['Fuel_Price'])
df = df.dropna(subset='Fuel_Price')
df.head(3)-Temperature 이상치 제거
# Temperature 이상치 제거
pct25 = df['Temperature'].quantile(.25)
pct75 = df['Temperature'].quantile(.75)
iqr = pct75 - pct25
pct25 - 1.5 * iqr # 하한
pct75 + 1.5 * iqr # 상한
df['Temperature'] = np.where((df['Temperature']<pct25 - 1.5 * iqr) | (df['Temperature']>pct75 + 1.5 * iqr), np.nan, df['Temperature'])
df = df.dropna(subset='Temperature')
df.head(3)-Unemployment 이상치 제거
# Unemployment 이상치 제거
pct25 = df['Unemployment'].quantile(.25)
pct75 = df['Unemployment'].quantile(.75)
iqr = pct75 - pct25
pct25 - 1.5 * iqr # 하한
pct75 + 1.5 * iqr # 상한
df['Unemployment'] = np.where((df['Unemployment']<pct25 - 1.5 * iqr) | (df['Unemployment']>pct75 + 1.5 * iqr), np.nan, df['Unemployment'])
df = df.dropna(subset='Unemployment')
df.head(3)5. 스케일링
데이터의 질이 좋지 못하다고 생각해서 총 두가지의 스케일링을 진행!
▶ 최소최대(MinMax) 스케일링
1. Date가 datetime 형식이라 표준화 스케일링이 불가해 제거함
df = df.drop(columns=['Date'])2. 데이터 분할
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
#데이터 분할
X_train,X_test,y_train,y_test = train_test_split(df[['Dept','Size','Store','CPI','Temperature','Unemployment','Fuel_Price','month']],df['Weekly_Sales'],test_size=0.3,random_state=42)3. 데이터 정규화(학습데이터, 테스트 데이터)
#데이터 정규화(학습데이터, 테스트데이터)
mm_scaler = MinMaxScaler()
X_train_scaled = mm_scaler.fit_transform(X_train)
X_test_scaled = mm_scaler.transform(X_test)
print("X_train_scaled sample:")
print(X_train_scaled[:3])
print("X_test_scaled sample:")
print(X_test_scaled[:3])▶ 표준화 스케일링
(최소최대 스케일링과 거의 동일하다!)
1. Date가 datetime 형식이라 표준화 스케일링이 불가해 제거함
df = df.drop(columns=['Date'])2. 데이터 분할
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(df[['Dept','Size','Store','CPI','Temperature','Unemployment','Fuel_Price','month']],df['Weekly_Sales'],test_size=0.3,random_state=42)3. 데이터 정규화 해주기
mm_scaler = StandardScaler()
X_train_scaled = mm_scaler.fit_transform(X_train)
X_test_scaled = mm_scaler.transform(X_test)
# X_train_scaled과 X_test_scaled의 결과 출력
print("X_train_scaled sample:")
print(pd.DataFrame(X_train_scaled, columns=X_train.columns).head())
print("\nX_test_scaled sample:")
print(pd.DataFrame(X_test_scaled, columns=X_test.columns).head())6. 모델링
스케일링까지 끝났다면 이제 러신머닝을 사용해서 이 데이터의 성능이 어떤지 설명력이 강한지 약한지 알아 볼 수 있다.
나는 회귀의 가장 기본적인 선형회귀와 릿지회귀를 사용해 분석을 해봤다.
▶ 선형회귀 :
- 모델이 간단하기 때문에 구현과 해석이 쉽다
- 같은 이유로 모델링하는 데 오랜 시간이 걸리지 않는다
1. 선형회귀 모델 생성 및 학습하기
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
lr_model = LinearRegression()
lr_model.fit(X_train_scaled, y_train)
2. 예측하기
y_train_pred_lr = lr_model.predict(X_train_scaled)
y_test_pred_lr = lr_model.predict(X_test_scaled)3. 성능 평가 - 학습 데이터
train_mse_lr = mean_squared_error(y_train, y_train_pred_lr)
train_rmse_lr = train_mse_lr ** 0.5
train_r2_lr = r2_score(y_train, y_train_pred_lr)4. 성능 평가 - 테스트 데이터
test_mse_lr = mean_squared_error(y_test, y_test_pred_lr)
test_rmse_lr = test_mse_lr ** 0.5
test_r2_lr = r2_score(y_test, y_test_pred_lr)5. 결과 출력
print("Training Set:")
print(f" - MSE: {train_mse_lr:.2f}")
print(f" - RMSE: {train_rmse_lr:.2f}")
print(f" - R-squared (R²) Score: {train_r2_lr:.2f}")
print("Test Set:")
print(f" - MSE: {test_mse_lr:.2f}")
print(f" - RMSE: {test_rmse_lr:.2f}")
print(f" - R-squared (R²) Score: {test_r2_lr:.2f}")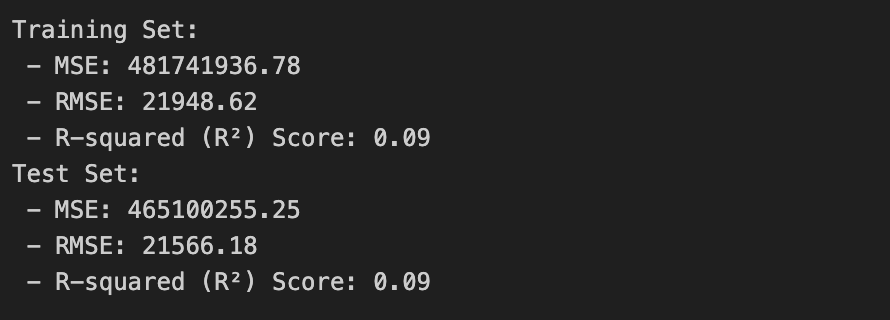
-Mean Squared Error(MSE) : 예측 값과 실제 값 사이의 평균 제곱 오차 값이 작을수록 좋다
-R-squared score : 1에 가까울수록 모델이 데이터를 잘 설명하는 것
--> 전체적으로 봤을때도 값들이 너무 크거나 1보다 작기 때문에 모델 성능이 좋지 못하다는 것을 알 수 있다
좀 더 직관적으로 보기 위해 시각화를 해봤다.
학습 데이터와 테스트 데이터를 시각화하여 두개를 나타냈다.
# 학습 데이터와 테스트 데이터 시각화
plt.figure(figsize=(14, 6))
# 학습 데이터 시각화
plt.subplot(1, 2, 1)
plt.scatter(y_train, y_train_pred_lr, color='blue', label='Predicted vs Actual')
plt.plot([y_train.min(), y_train.max()], [y_train.min(), y_train.max()], color='red', linestyle='--')
plt.title("Training Data: Predicted vs Actual")
plt.xlabel("Actual")
plt.ylabel("Predicted")
plt.legend()
# 테스트 데이터 시각화
plt.subplot(1, 2, 2)
plt.scatter(y_test, y_test_pred_lr, color='green', label='Predicted vs Actual')
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], color='red', linestyle='--')
plt.title("Test Data: Predicted vs Actual")
plt.xlabel("Actual")
plt.ylabel("Predicted")
plt.legend()
plt.tight_layout()
plt.show()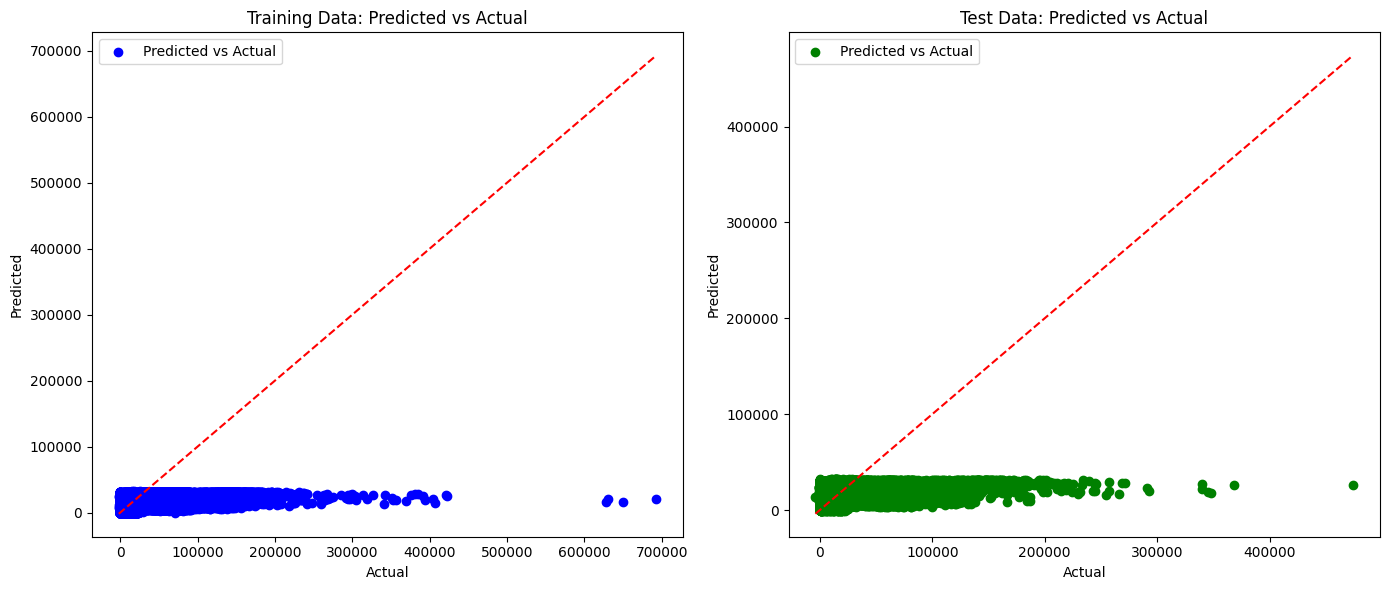
- 설명해야함
▶ 릿지회귀:
- 선형회귀 모델에 L2 정규화를 적용한 모델로 오버피팅을 억제하는 효과
1. 릿지 회귀 모델 생성 및 학습
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_absolute_error
ridge_model = Ridge(alpha=0.1)
ridge_model.fit(X_train_scaled, y_train)
2. 예측
y_train_pred_ridge = ridge_model.predict(X_train_scaled)
y_test_pred_ridge = ridge_model.predict(X_test_scaled)3. 성능 평가 - 학습 데이터
train_mse_ridge = mean_squared_error(y_train, y_train_pred_ridge)
train_rmse_ridge = train_mse_ridge ** 0.5
train_r2_ridge = r2_score(y_train, y_train_pred_ridge)
train_mae_ridge = mean_absolute_error(y_train, y_train_pred_ridge)4. 성능 평가 - 테스트 데이터
test_mse_ridge = mean_squared_error(y_test, y_test_pred_ridge)
test_rmse_ridge = test_mse_ridge ** 0.5
test_r2_ridge = r2_score(y_test, y_test_pred_ridge)
test_mae_ridge = mean_absolute_error(y_test, y_test_pred_ridge)5. 결과 출력
print("Training Set:")
print(f" - MSE: {train_mse_ridge:.2f}")
print(f" - RMSE: {train_rmse_ridge:.2f}")
print(f" - R-squared (R²) Score: {train_r2_ridge:.2f}")
print(f" - MAE: {train_mae_ridge:.2f}")
print("Test Set:")
print(f" - MSE: {test_mse_ridge:.2f}")
print(f" - RMSE: {test_rmse_ridge:.2f}")
print(f" - R-squared (R²) Score: {test_r2_ridge:.2f}")
print(f" - MAE: {test_mae_ridge:.2f}")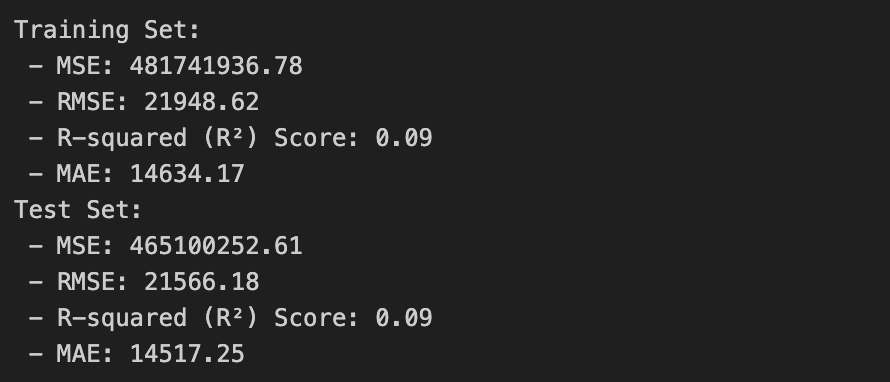
릿지회귀도 선형회귀와 값의 거의 동일하다 그 말은 즉슨, 모델 성능이 좋지 않다는 뜻이다.
모델 성능이 좋지 못해 최적의 알파값을 찾기 위해 그리드서치(하이퍼 파라미터)를 통해 최적의 값을 찾아봤다.
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error, r2_score
ridge = Ridge()
params = {'alpha' : [0.1, 1, 10, 100]}
gridsearch = GridSearchCV(ridge, param_grid= params)
gridsearch.fit(X_train_scaled, y_train)
print(f"Best alpha: {gridsearch.best_params_['alpha']}")
print(f"Best R-squared score on training data : {gridsearch.best_score_:.2f}")
최적의 알파값은 10이 나왔지만 최적의 R-squared는 변동없이 작은 숫자인 0.09로 변함이 없었다.
하지만 최적의 알파값을 찾았기 때문에 다시 모델을 돌려보았다.
# 최적의 값으로 다시 넣어보기
ridge_model = Ridge(alpha=10)
ridge_model.fit(X_train_scaled, y_train)
y_train_pred_ridge = ridge_model.predict(X_train_scaled)
y_test_pred_ridge = ridge_model.predict(X_test_scaled)
# 성능 평가 - 학습 데이터
train_mse_ridge = mean_squared_error(y_train, y_train_pred_ridge)
train_rmse_ridge = train_mse_ridge ** 0.5
train_r2_ridge = r2_score(y_train, y_train_pred_ridge)
# 성능 평가 - 테스트 데이터
test_mse_ridge = mean_squared_error(y_test, y_test_pred_ridge)
test_rmse_ridge = test_mse_ridge ** 0.5
test_r2_ridge = r2_score(y_test, y_test_pred_ridge)
print("Training Set:")
print(f" - MSE: {train_mse_ridge:.2f}")
print(f" - RMSE: {train_rmse_ridge:.2f}")
print(f" - R-squared (R²) Score: {train_r2_ridge:.2f}")
print("Test Set:")
print(f" - MSE: {test_mse_ridge:.2f}")
print(f" - RMSE: {test_rmse_ridge:.2f}")
print(f" - R-squared (R²) Score: {test_r2_ridge:.2f}")
눈을 크게 뜨고 찾아보면 조금 더 나아지긴 했으나 크게 달라진 건 없었고 여전히 성능은 좋지 않았다.
릿지회귀도 직관적으로 보기위해 시각화를 해봤다.
# 학습 데이터와 테스트 데이터 시각화
plt.figure(figsize=(14, 6))
# 학습 데이터 시각화
plt.subplot(1, 2, 1)
plt.scatter(y_train, y_train_pred_ridge, color='blue', label='Predicted vs Actual')
plt.plot([y_train.min(), y_train.max()], [y_train.min(), y_train.max()], color='red', linestyle='--')
plt.title("Training Data: Predicted vs Actual")
plt.xlabel("Actual")
plt.ylabel("Predicted")
plt.legend()
# 테스트 데이터 시각화
plt.subplot(1, 2, 2)
plt.scatter(y_test, y_test_pred_ridge, color='green', label='Predicted vs Actual')
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], color='red', linestyle='--')
plt.title("Test Data: Predicted vs Actual")
plt.xlabel("Actual")
plt.ylabel("Predicted")
plt.legend()
plt.tight_layout()
plt.show()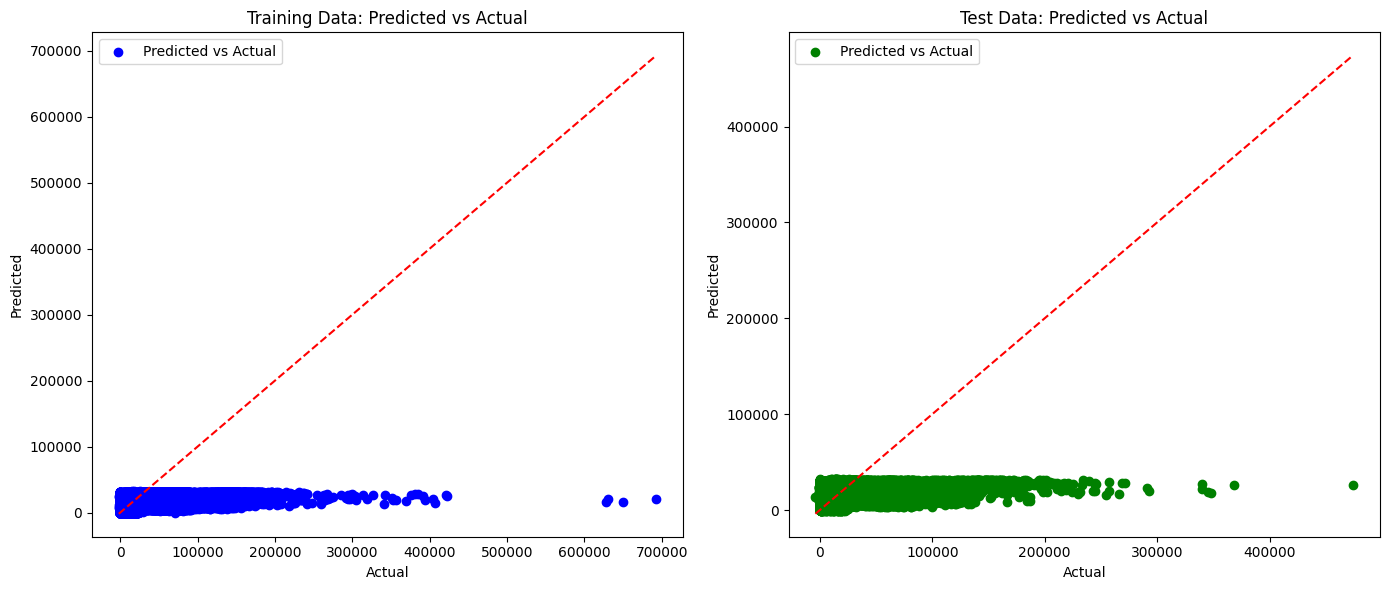
시각화한만 봐도 좋지 못하다는 것을 확 체감할 수 있다.
그래서 나는 선형회귀와 릿지회귀의 값이 거의 동일하기에 같이 넣어 비교를 한다면 눈에 확 들어오지 않을까 하고 두개를 이용해 시각화를 해봤다.
import matplotlib.pyplot as plt
# 실제 값 vs 예측 값 플롯 (선형 회귀 vs 릿지 회귀)
plt.figure(figsize=(14, 12))
# 학습 데이터에 대한 비교
plt.subplot(2, 2, 1) # 첫번째 위치(첫번째 행의 첫번째 열)을 의미
plt.scatter(y_train, y_train_pred_lr, alpha=0.3, label='Linear Regression', color='blue')
plt.scatter(y_train, y_train_pred_ridge, alpha=0.3, label='Ridge Regression', color='orange')
plt.plot([min(y_train), max(y_train)], [min(y_train), max(y_train)], color='red', linestyle='--')
plt.title('Training Set: Actual vs Predicted')
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.legend()
plt.grid(True)
# 테스트 데이터에 대한 비교
plt.subplot(2, 2, 2) #두번째 위치(첫번째 행의 두번째 열)을 의미
plt.scatter(y_test, y_test_pred_lr, alpha=0.3, label='Linear Regression', color='blue')
plt.scatter(y_test, y_test_pred_ridge, alpha=0.5, label='Ridge Regression', color='orange')
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], color='red', linestyle='--')
plt.title('Test Set: Actual vs Predicted')
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
잘 보지 않으면 보이지 않을정도로 선형회귀와 릿지회귀의 모양이 일치했다.
선형회귀는 파란색으로 지정했고 릿지회귀는 주황색으로 지정했지만 거의 동일하여 잘 보이지 않는다.
이것을 보아
- 점들이 선에 가까이 분포하지 않는 것으로 봐선, 잘 예측하지 못하고 있다.
- 학습 데이터와 테스트 데이터가 거의 동일할 정도로 비슷하여 어느 모델이 더 나은지 확인불가 --> 둘 다 좋지 못한 성능
'Project' 카테고리의 다른 글
| [실전 프로젝트] 아마존 데이터 속으로 떠나는 인사이트 모험1 (6) | 2024.09.27 |
|---|---|
| [심화 프로젝트] 이커머스 주간 판매량 예측3 (0) | 2024.08.30 |
| [심화프로젝트] 이커머스 주간 판매량 예측1 (0) | 2024.08.23 |
| [기초 프로젝트] END! + 피드백 (0) | 2024.07.29 |
| [기초 프로젝트] DAY 3 (1) | 2024.07.26 |
